Cách để Tìm số Armstrong

Số Armstrong là một khái niệm quan trọng trong lĩnh vực mã hóa và giải mã để bảo mật dữ liệu.

Khái niệm chung về xử lý các chữ số của một số là một kỹ thuật cơ bản. Bạn có thể giải quyết nhiều nhiệm vụ bằng phương pháp này, chẳng hạn như tính tổng các chữ số, lấy tích các chữ số, đếm các chữ số và đảo ngược một số.

Nhưng số Armstrong là gì và làm thế nào để bạn kiểm tra một số?

Số Armstrong là gì?

Số Amstrong là số có tổng lập phương các chữ số của nó bằng chính số đó. Ví dụ: 153 là số Armstrong. Nếu bạn lấy riêng các chữ số của 153 và chia chúng thành lập phương:

(1×1×1) + (5×5×5) + (3×3×3)

Sau đó cộng kết quả:

1 + 125 + 27

Bạn sẽ nhận được 153, giống như số ban đầu.

Một thuật toán để tìm một số Armstrong

Viết một thuật toán là bước đầu tiên để thực hiện bất kỳ chương trình nào. Bạn có thể sử dụng thuật toán làm tài liệu tham khảo để viết mã giả, sau đó triển khai nó bằng ngôn ngữ lập trình bạn muốn. Một thuật toán cung cấp cho bạn một loạt hướng dẫn chính xác để làm theo, loại bỏ các lỗi logic và giúp việc triển khai trở nên đơn giản hơn.

Đây là thuật toán để tìm xem một số có phải là Armstrong hay không:

1. Khai báo các biến sum, temp, n, r
2. Lấy giá trị của n từ người dùng
3. Khởi tạo biến tổng thành 0 và sao lưu n dưới dạng temp = n
4. Lặp lại các bước 5 – 7 khi n > 0
5. r = n % 10
6. tổng = tổng + lập phương của mỗi chữ số (r × r × r)
7. n = n / 10
8. Nếu tổng bằng tạm thời, hiển thị “Số là số Armstrong”
9. Khác, hiển thị “Số không phải là Số Armstrong”

Mã giả để thực hiện thuật toán Armstrong

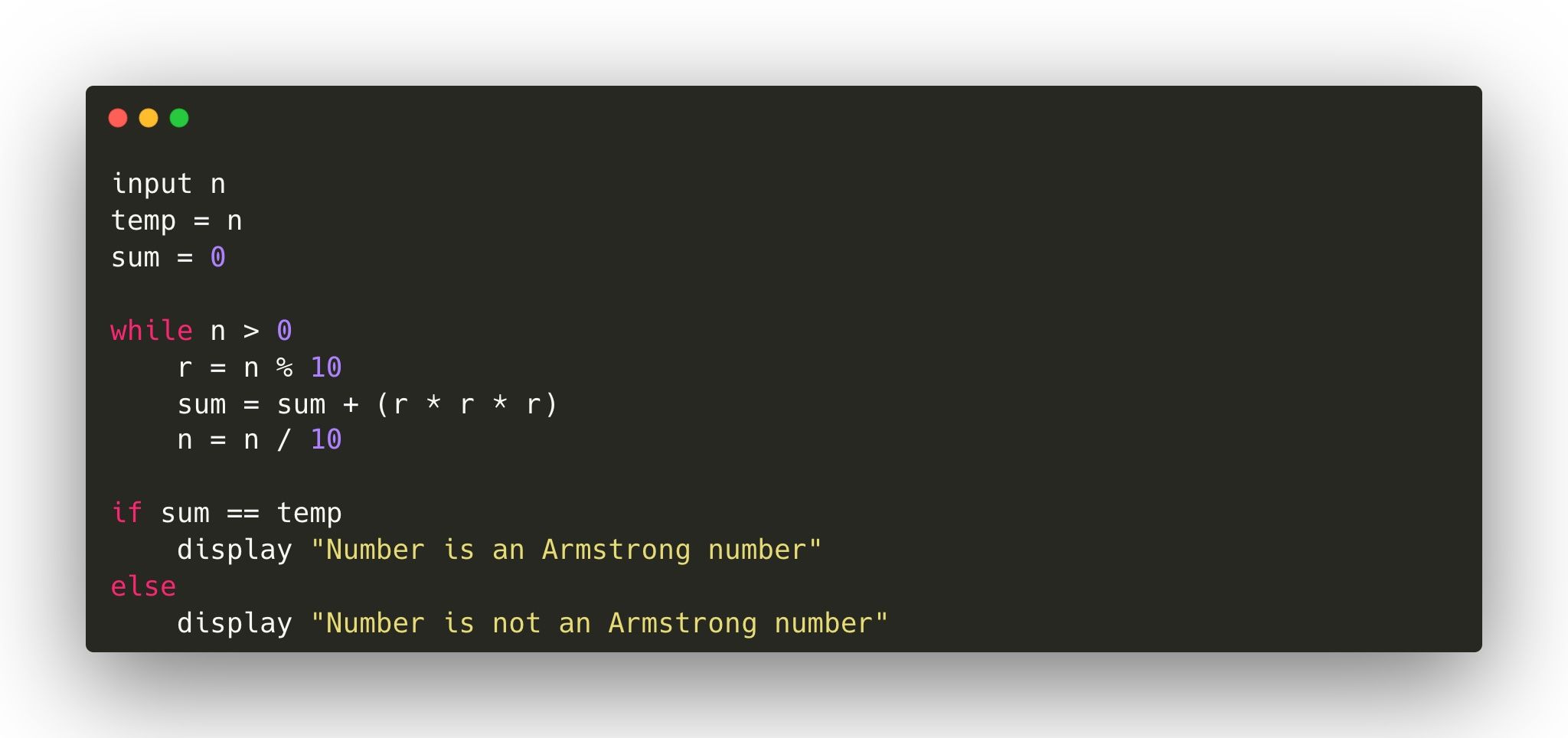
Mã giả có thể là một bước hữu ích trong việc thiết kế triển khai thuật toán. Viết mã giả giúp bạn dễ dàng chuyển đổi nó thành mã bằng bất kỳ ngôn ngữ lập trình nào. Đây là mã giả để triển khai số Armstrong:

Chương trình Armstrong trong C

Quan sát mã giả ở trên và chuyển đổi từng câu lệnh thành mã C.

Bắt đầu bằng cách nhập stdio.h để thực hiện các thao tác nhập xuất. khai báo chính chức năng và bắt đầu thực hiện logic của chương trình. Sử dụng N để lưu trữ số đầu vào, r để lưu trữ các chữ số riêng lẻ của số, Tổng để lưu trữ tổng lập phương của các chữ số, và nhiệt độ để lưu trữ một bản sao của số.

Sử dụng bản inf chức năng yêu cầu người dùng nhập số. Sử dụng quét chức năng để đọc số và lưu trữ nó trong biến N. %d là công cụ xác định định dạng thập phân để lấy một số nguyên làm đầu vào.

Xóa mọi giá trị rác bằng cách khởi tạo tổng bằng 0 và sao lưu n làm tạm thời.

#include <stdio.h>

int main()
{
int n, r, sum, temp;
printf("Please enter a number: ");
scanf("%d", &n);
sum = 0; temp = n;

khai báo một trong khi vòng lặp chạy cho đến khi số bằng 0 hoặc ít hơn. Bên trong vòng lặp là một quy trình gồm ba bước mà bạn có thể sử dụng trong nhiều tác vụ lập trình khác. Ba bước là:

1. Lấy từng chữ số của một số bằng cách lấy mô đun của số đó với 10. Khi bạn chia một số bất kỳ cho 10, phần còn lại chính là chữ số cuối cùng. Ví dụ: khi bạn chia 153 cho 10, kết quả số nguyên là 15 và mô đun là 3.
2. Khi bạn có từng chữ số, bạn có thể thực hiện thao tác mong muốn của mình. Để tìm một số Armstrong, thao tác mong muốn là tổng lập phương của các chữ số của số đó. Lấy lập phương của chữ số r và thêm nó vào biến tổng.
3. Loại bỏ chữ số cuối cùng của số bằng cách chia nó cho 10. Khi chia cho 10, bạn nhận được thương, trong trường hợp này là 15.

while (n > 0) {
r = n % 10;
sum = sum + (r * r * r);
n = n / 10;
}

Kiểm tra xem tổng thu được có bằng số ban đầu không. Nếu chúng bằng nhau, thì số đó thực sự là số Armstrong, nếu không thì không phải.

if (temp == sum)
printf("Number is an Armstrong numbern");
else
printf("Number is not an Armstrong numbern");

return 0;
}

Các ứng dụng khác của thuật toán chung

Bằng cách thay đổi bước hai trong logic ba bước ở trên, bạn có thể triển khai nhiều chương trình khác nhau.

1. Tổng, tích các chữ số của số

Để lấy tổng các chữ số của một số, chỉ cần thay thế dòng bằng:

sum = sum + r;

Đối với sản phẩm, hãy khai báo biến prod là 1 và thay thế tổng cộng bằng ký hiệu phép nhân:

prod = prod * r;

2. Đếm chữ số của số

Để đếm các chữ số của một số, chỉ cần khởi tạo một biến đếm bằng không, bỏ qua bước một và tăng nó cho đến khi n bằng không. Việc thực hiện vòng lặp sẽ như thế này:

while (n > 0) {
count++;
n = n / 10;
}

3. Số đảo ngược, số Palindrome

Để đảo ngược một số, hãy khởi tạo biến rev thành một và cộng nó sau khi nhân với mười:

rev = (rev * 10) + r;

Khi bạn nhận được số ngược của một số, hãy so sánh nó với bản sao của chính số ban đầu. Nếu số đảo ngược bằng chính số đó thì đó là số Palindrome.

4. Chữ số nhỏ nhất và lớn nhất của một số

Khởi tạo một biến min là chín và so sánh nó với chữ số được trích ra từ bước một để tìm chữ số nhỏ nhất của một số. Bạn có thể thực hiện nó như:

if (r < min) {
min = r;
}

Tương tự, khởi tạo một biến max bằng 0 và so sánh nó với chữ số được trích xuất để tìm chữ số lớn nhất của một số. Bạn có thể thực hiện nó như:

if (r > max) {
max = r;
}

Đây là cách bạn có thể tìm thấy các chữ số lớn nhất và nhỏ nhất của một số.

5. Số đặc biệt

Có nhiều số khác, chẳng hạn như số Armstrong, mà bạn có thể tính toán. Chúng bao gồm số Neon, số Automorphic, số Krishnamurthy, số buzz, số hoàn hảo, số thân thiện và số nguyên tố sinh đôi.

Lập trình và Toán học

Toán học được sử dụng rộng rãi trong lập trình. Toán học nhị phân là cốt lõi của lập trình vì tất cả phần mềm bạn sử dụng ngày nay là sự kết hợp của các chữ số không và một. Tất cả dữ liệu bạn làm việc được lưu trữ ở định dạng nhị phân. Đại số tuyến tính được sử dụng trong các ứng dụng máy học, thuật toán đồ thị, tính toán lượng tử, v.v.

Giải tích, toán học rời rạc và thống kê được sử dụng rộng rãi trong giải quyết vấn đề và thiết kế thuật toán. Toán học nâng cao kỹ năng tính toán của bạn và là một phần thiết yếu của lập trình.